Analiza projektu inwestycyjnego z wykorzystaniem funkcji finansowych XNPV, XIRR oraz MIRR
Analiza projektu inwestycyjnego wymaga nie tylko bardzo obszernej wiedzy finansowej, lecz również wiedzy technicznej, bowiem wszelkie obliczenia dokonuje się w arkuszu kalkulacyjnym Excel. Wraz z rozwojem kolejnych wersji, Excel zaproponował kilka podstawowych, z punktu widzenia inwestycji, funkcji do wykorzystania przy ocenie projektu inwestycyjnego. Funkcje te to XNPV, XIRR oraz MIRR i odnoszą się do trzech kluczowych metryk obliczanych i analizowanych przy okazji oceny projektu. Niniejszy artykuł porusza kwestię budowy funkcji, ale również aspekty teoretyczne, jak istotę oraz wady i zalety kluczowych mierników.

Krótkie wprowadzenie teoretyczne do oceny projektów inwestycyjnych
Analitycy i inwestorzy, chcąc dokonać oceny projektu inwestycyjnego, skupiają się najczęściej na trzech podstawowych miarach. Są to:
- Wartość bieżąca netto (NPV) – obliczamy, dyskontując przyszłe przepływy pieniężne i odejmując od nich poniesione nakłady inwestycyjne. Jeśli NPV jest dodatnie, to znaczy, że projekt jest opłacalny.
- Wewnętrzna stopa zwrotu (IRR) – stopa procentowa, przy której wartość NPV = 0. Krótko mówiąc, jest to minimalna stopa zwrotu, przy której wychodzimy na zero.
- Modyfikowana wewnętrzna stopa zwrotu (MIRR) – jest to modyfikacja wskaźnika IRR, a zarazem stopa dyskontowa, dla której wartość końcowa inwestycji jest równa zaktualizowanej wartości nakładów inwestycyjnych. Jeśli MIRR jest większe od kosztu kapitału, to projekt jest opłacalny.
Funkcja XNPV – analiza Net Present Value przy nieregularnych przepływach pieniężnych
XNPV (Extended Net Present Value) to funkcja Excela, która umożliwia obliczenie wartości bieżącej netto dla przepływów pieniężnych o nieregularnych odstępach czasu. Tradycyjna funkcja NPV zakłada równe okresy między przepływami, natomiast jej nowsza wersja – funkcja XNPV – pozwala uwzględnić dokładne daty przepływów. Jest to oczywiście zmiana na plus z punktu widzenia użytkownika, bowiem rzadkością są projekty z regularnymi, przewidywalnymi przepływami. Z wady tej funkcji narodziła się właśnie funkcja XNPV. Spójrzmy na składnię:
=XNPV(stopa dyskontowa, przepływy, daty)
Stopa dyskontowa: jest to zakładana roczna stopa zwrotu, na podstawie której wartości przepływów są dyskontowane do wartości dzisiejszej.
Przepływy: jest to zakres danych zawierający wartości przepływów pieniężnych. Pierwsza wartość powinna być ujemna (koszt początkowy), a pozostałe dodatnie (przychody) lub ujemne (koszty).
Daty: zakres danych zawierający daty każdego przepływu.
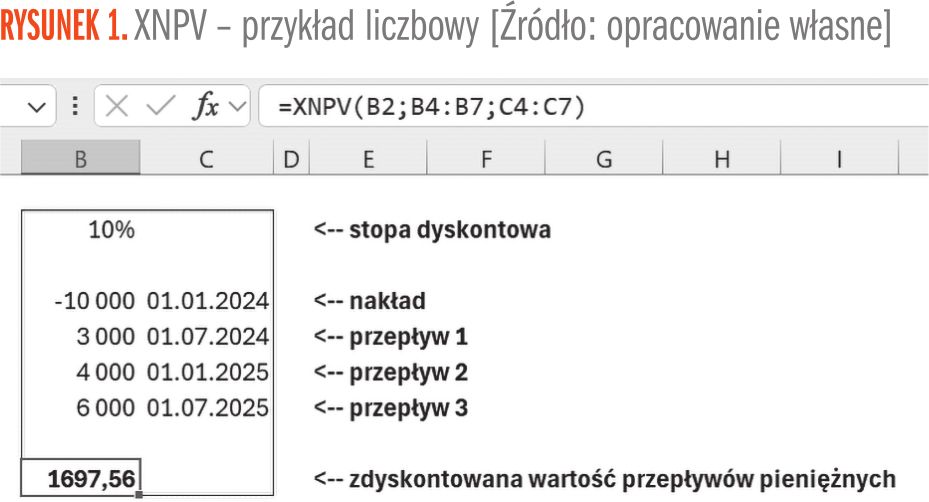
Funkcja XNPV – przykład liczbowy
Załóżmy, że mamy ocenić wartość NPV dla projektu, który wymaga inwestycji początkowej w kwocie 10.000 zł w dniu 1.01.2024 przy rocznej stopie dyskontowej 10% oraz generuje następujące przepływy pieniężne:
- 3000 zł – 1.07.2024
- 4000 zł – 1.01.2025
- 6000 zł – 1.07.2025
Używając formuły XNPV, należy uważać na chronologię. Należy ułożyć zestaw danych według dat, rozpoczynając od najwcześniejszego przepływu.
Zalety funkcji XNPV
-
Dokładność przy nieregularnych przepływach pieniężnych: XNPV pozwala uwzględnić dokładne daty przepływów pieniężnych, co zwiększa precyzję wyliczeń w przypadku projektów, które nie mają regularnych przepływów, np. kwartalnych lub półrocznych. Pozwala to uniknąć sytuacji, w której ocena projektu jest deprecjonowana z racji przyjęcia założenia stałych, regularnych przepływów.
Wykorzystałeś swój limit bezpłatnych treści
Pozostałe 70% artykułu dostępne jest dla zalogowanych użytkowników portalu. Zaloguj się, wybierz plan abonamentowy albo kup dostęp do artykułu/dokumentu.






 Zaloguj się
Zaloguj się